Cách Tính Diện Tích Tam Giác Thường, Cân,Vuông, Đều Và Ví Dụ

Cách tính và công thức tính diện tích tam giác là kiến thức cơ bản trong toán học, giúp bạn áp dụng để giải nhiều bài toán khác nhau cũng như các lĩnh vực khác nhau trong cuộc sống. Để biết thêm thông tin về cách tính diện tích các tam giác trong hình học, bạn có thể tham khảo ngay bài viết hướng dẫn và ví dụ chi tiết dưới đây của g4me.net. 

Nhận biết các loại tam giác trong hình học 

Tam giác là một trong số những hình học phẳng của toán học, có 3 điểm không thẳng hàng nối lại với nhau tạo thành một hình có 3 cạnh. Đây cũng là hình đa giác có số cạnh ít nhất của hình học phẳng, dấu hiệu nhận biết cơ bản bao gồm 3 đỉnh và 3 cạnh. 

Ví dụ cho một hình có 3 đỉnh A, B, C và 3 cánh là AB, AC và BC sẽ tạo ra được một hình tam giác ABC. Người ta sẽ dựa vào số đo các góc cũng như đặc điểm của cạnh bên để xác định các loại tam giác khác nhau, cụ thể: 

• Tam giác thường: Là tam giác có các cạnh và các góc không bằng nhau, không có góc nào 90 độ, còn được coi là trường hợp đặc biệt. 
• Tam giác cân: Là tam giác có hai cạnh bên bằng nhau, góc được tạo bởi hai cạnh này được gọi là góc đỉnh, còn lại là góc đáy. 
• Tam giác đều: Trường hợp tam giác có 3 cạnh và 3 góc bằng nhau (cùng bằng 60 độ) thì được coi là tam giác đều. 
• Tam giác vuông: Trong một hình tam giác có một góc bằng 90 độ thì được gọi là tam giác vuông, nếu có hai cạnh bằng nhau và 1 góc bằng 90 độ thì được gọi là tam giác vuông cân. 
• Tam giác tù: Hình tam giác sở hữu một góc trong lớn hơn 90 độ và một góc nhọn (bên ngoài) nhỏ hơn 90 độ. 
• Tam giác nhọn: Tam giác sở hữu ba góc nhọn (ba góc trong) đều nhỏ hơn 90 độ và các góc từ đều lớn hơn 90 độ. 

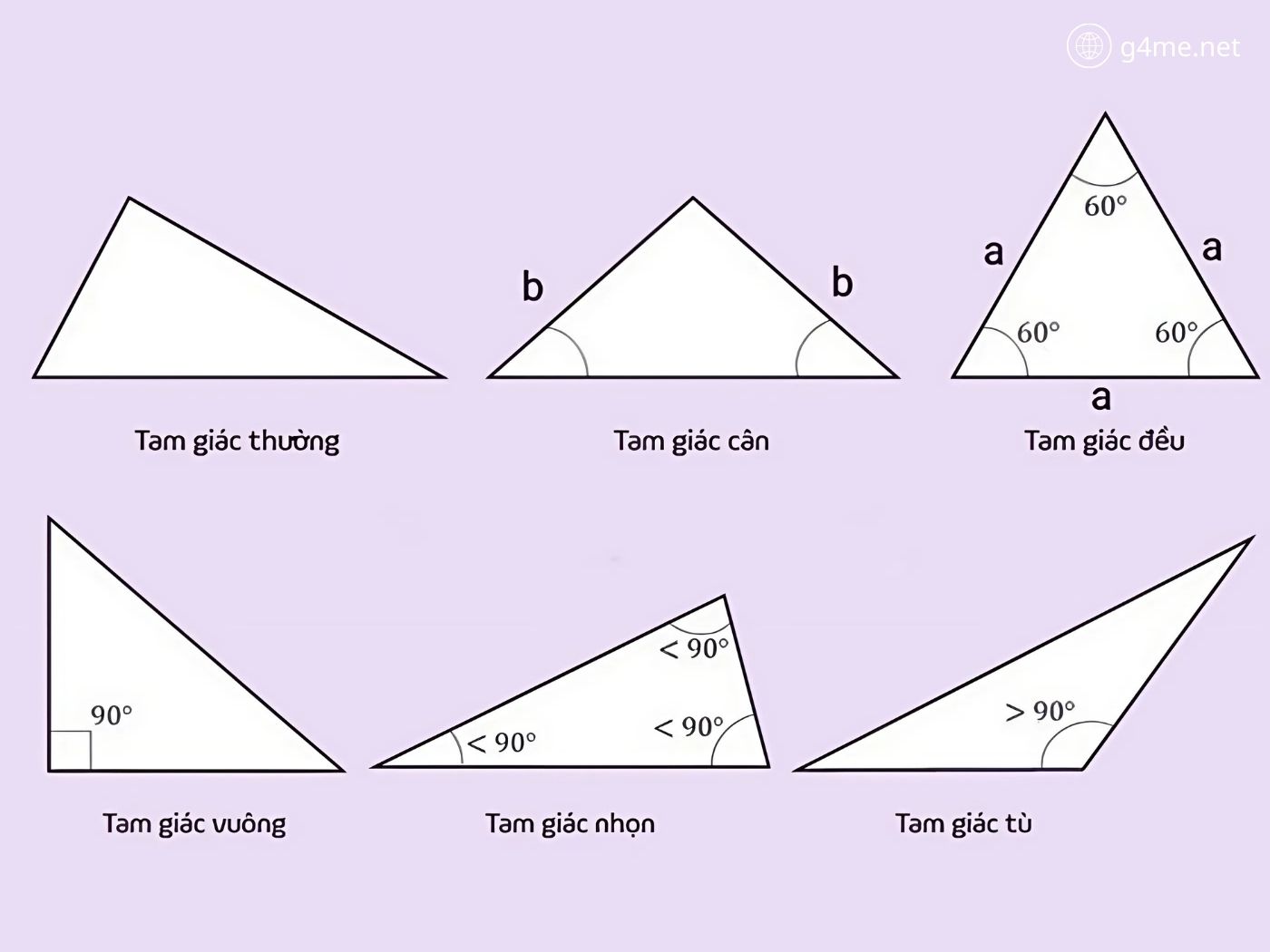Nhận biết các hình tam giác trong toán học

Công thức tính diện tích hình tam giác và ví dụ thực tế 

Cách tính diện tích hình tam giác không quá khó, bạn có thể áp dụng công thức là có thể tính toán chính xác. Tuy nhiên công thức diện tích này sẽ thay đổi tùy thuộc vào tích chất của từng hình tam giác khác nhau, cụ thể: 

Công thức tính diện tích tam giác thường 

Tam giác thường là tam giác có 3 cạnh và 3 góc không bằng nhau, nếu bạn muốn tính diện tích thì bắt buộc phải kẻ thêm một đường cao  từ đỉnh xuống cạnh đối diện. 

Công thức S = ½ (a x h) 

Trong đó 

• S = diện tích tam giác
• a = độ dài của một cạnh bất kỳ của tam giác 
• h = chiều cao hạ từ đỉnh đối diện xuống cạnh đáy

Ví dụ: Cho một hình tam giác thường ABC có cạnh đáy BC = 9 và chiều cao hạ từ A xuống BC là 3. Tính diện tích tam giác ABC. 

Lời giải: Gọi đường cao hạ từ A xuống BC là AH, khi đó ta có diện tích tam giác ABC là:  S =½ x (a x h) = ½ x (9 x 3) =  13.5cm2. 

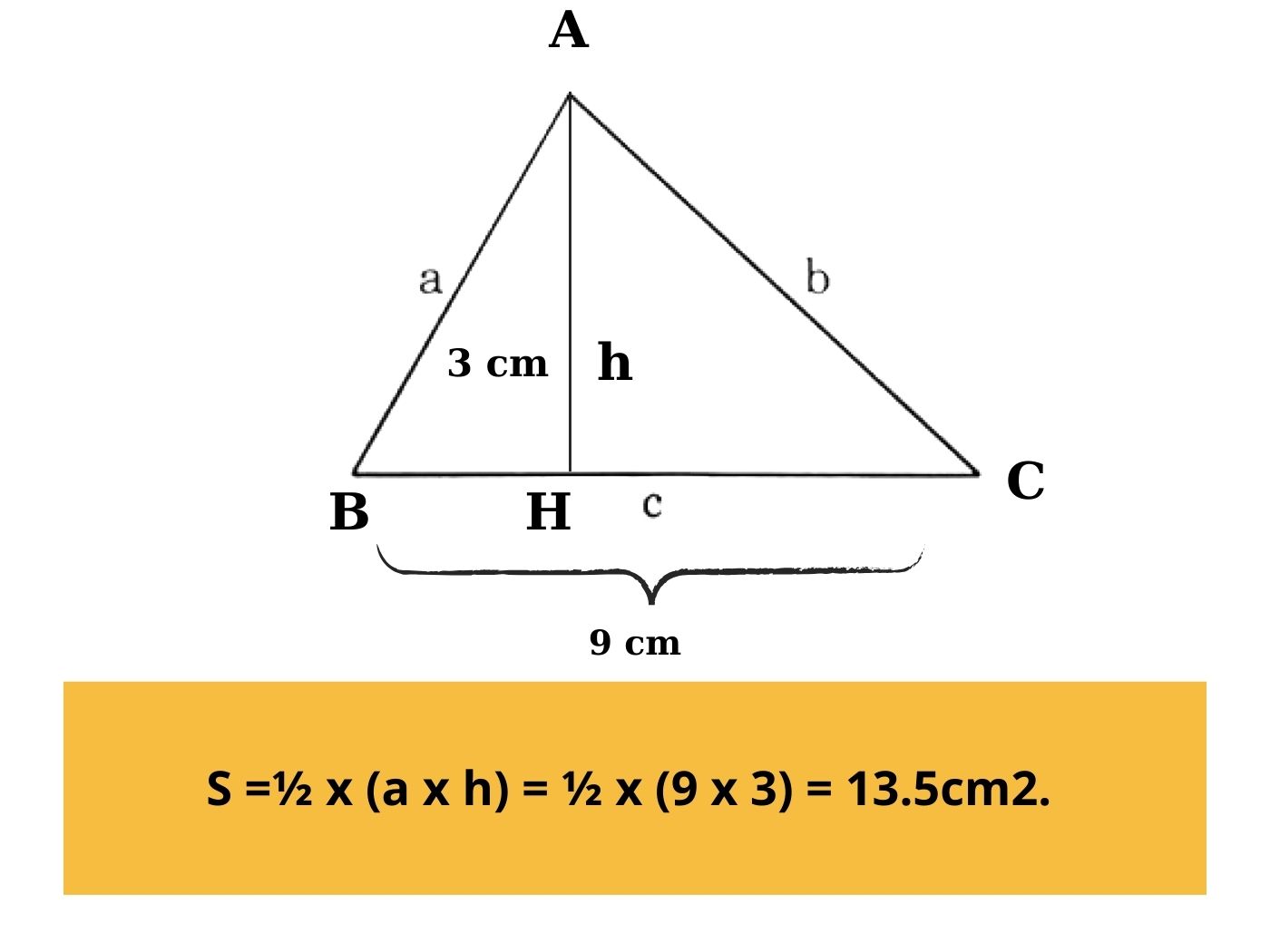Công thức tính diện tích tam giác thường

Cách tính diện tích tam giác cân 

Tam giác cân có hai cạnh bằng nhau và hai góc chứa hai cạnh còn lại bằng nhau, khi đó công thức tính diện tích tam giác cân là: 

Xem thêm: Cách Học Giỏi Toán Cho Người Mất Gốc – Lộ trình học Toán từ số 0

Công thức S = (a x h)/2 

Trong đó 

• S: Diện tích tam giác cân 
• a: Độ dài cạnh đáy (không dùng hai cạnh bên bằng nhau) 
• h: chiều cao hạ từ đỉnh đối diện xuống cạnh đáy 

Ví dụ: Cho một hình tam giác cân ABC có cạnh đáy BC = 9, đường cao hạ từ đỉnh A là 5, hãy tính diện tích tam giác. 

Lời giải: Gọi đường cao hạ từ đỉnh A xuống cạnh đáy BC là AH, khi đó diện tích tam giác ABC là: S = (axh)/2 = (BC x AH)/2 = (9 x 5)/2= 22,5cm2. 

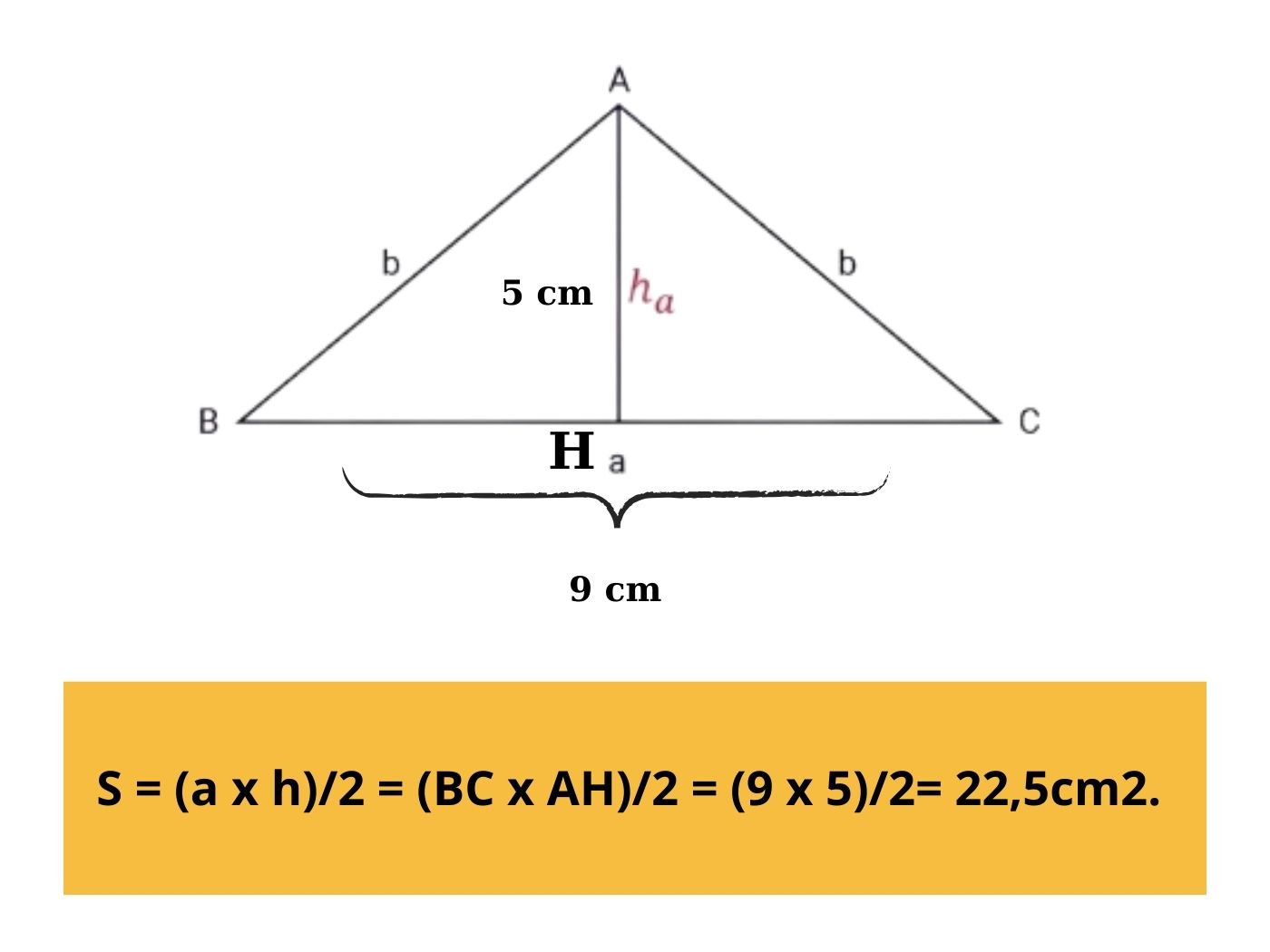Cách tính diện tích tam giác cân

Cách tính diện tích tam giác vuông cân 

Tam giác vuông cân là hình tam giác có hai cạnh đều và một góc là góc vuông bằng 90 độ. Khi đó công thức tính diện tích tam giác vuông cân là: 

Công thức S = (a²)/2

Trong đó: 

• S: Diện tích tam giác vuông cân 
• a: Độ dài cạnh góc vuông 

Ví dụ: Cho hình tam giác vuông cân có cạnh góc vuông AB = 8, yêu cầu hãy tính diện tích tam giác ABC. 

Lời giải: Áp dụng công thức tính diện tích tam giác vuông cân ta có S =  (a²)/2 = (AB^2)/2 = (8^2)/2 = 32 (cm2). 

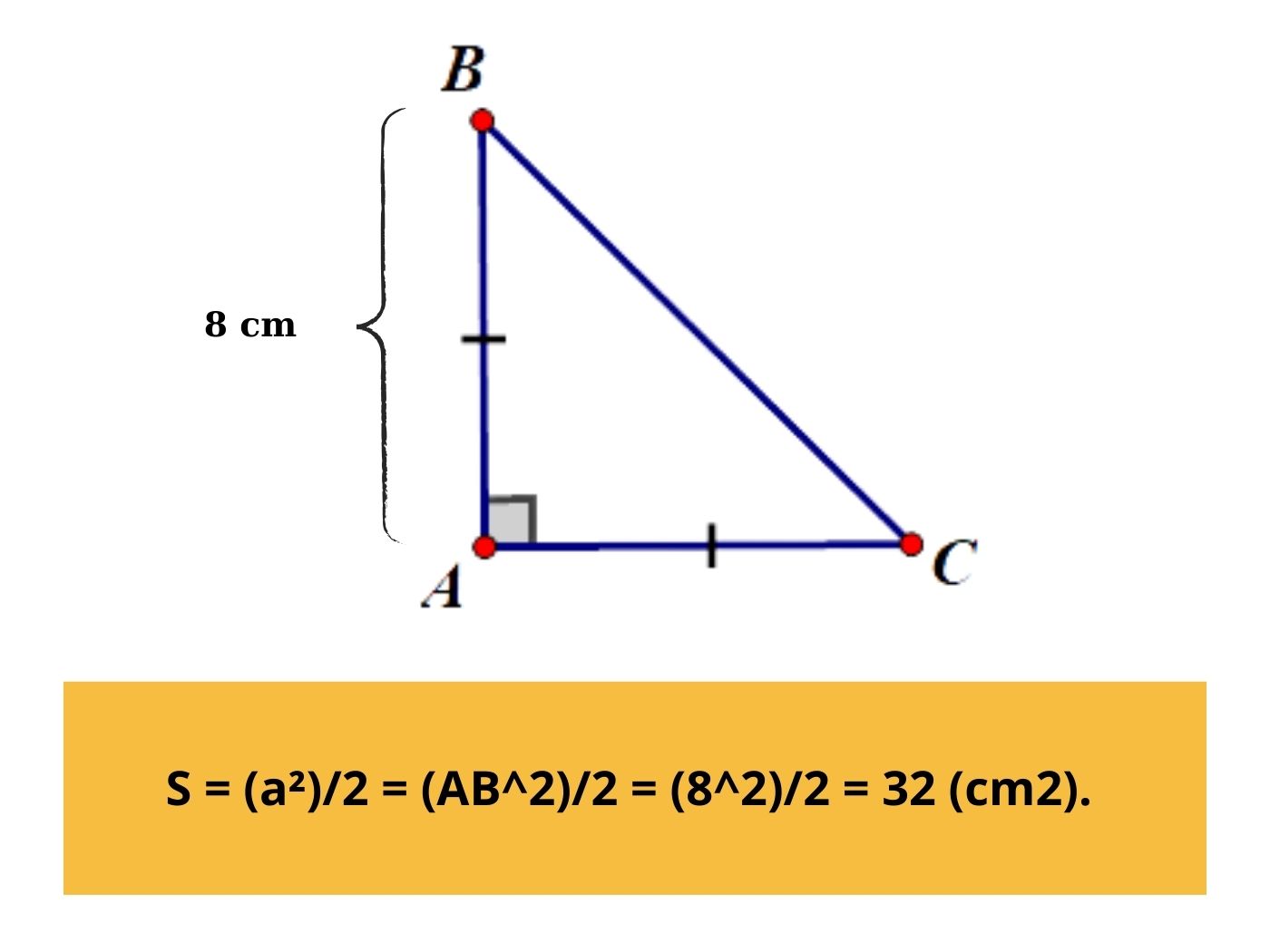Hướng dẫn tính diện tích hình tam giác vuông cân

Cách tính diện tích tam giác đều 

Tam giác đều có 3 cánh AB, AC và BC bằng nhau, các góc A, B, C bằng nhau, khi đó công thức tính diện tích tam giác là: 

Công thức S = ½ x a x h 

Trong đó 

• S: Diện tích tam giác đều
• a: Độ dài một cạnh bất kỳ của tam giác 
• h: Đường cao hạ từ đỉnh xuống cạnh đối diện  

Công thức mở rộng: Khi biết một cạnh của tam giác đều nhưng không biết chiều cao, bạn có thể áp dụng công thức tính diện tích S = (a² x √3) / 4. 

Ví dụ: Cho hình tam giác đều ABC có cạnh AB = 6 và chiều cao là 3√3, tính diện tích hình tam giác đều đã cho. 

Công thức 1: S = ½ x a x h = ½ (6 x 3√3) = 9√3 cm²

Công thức 2: S =  (a² x √3) / 4 = (6² x √3) / 4 = 9√3 cm²

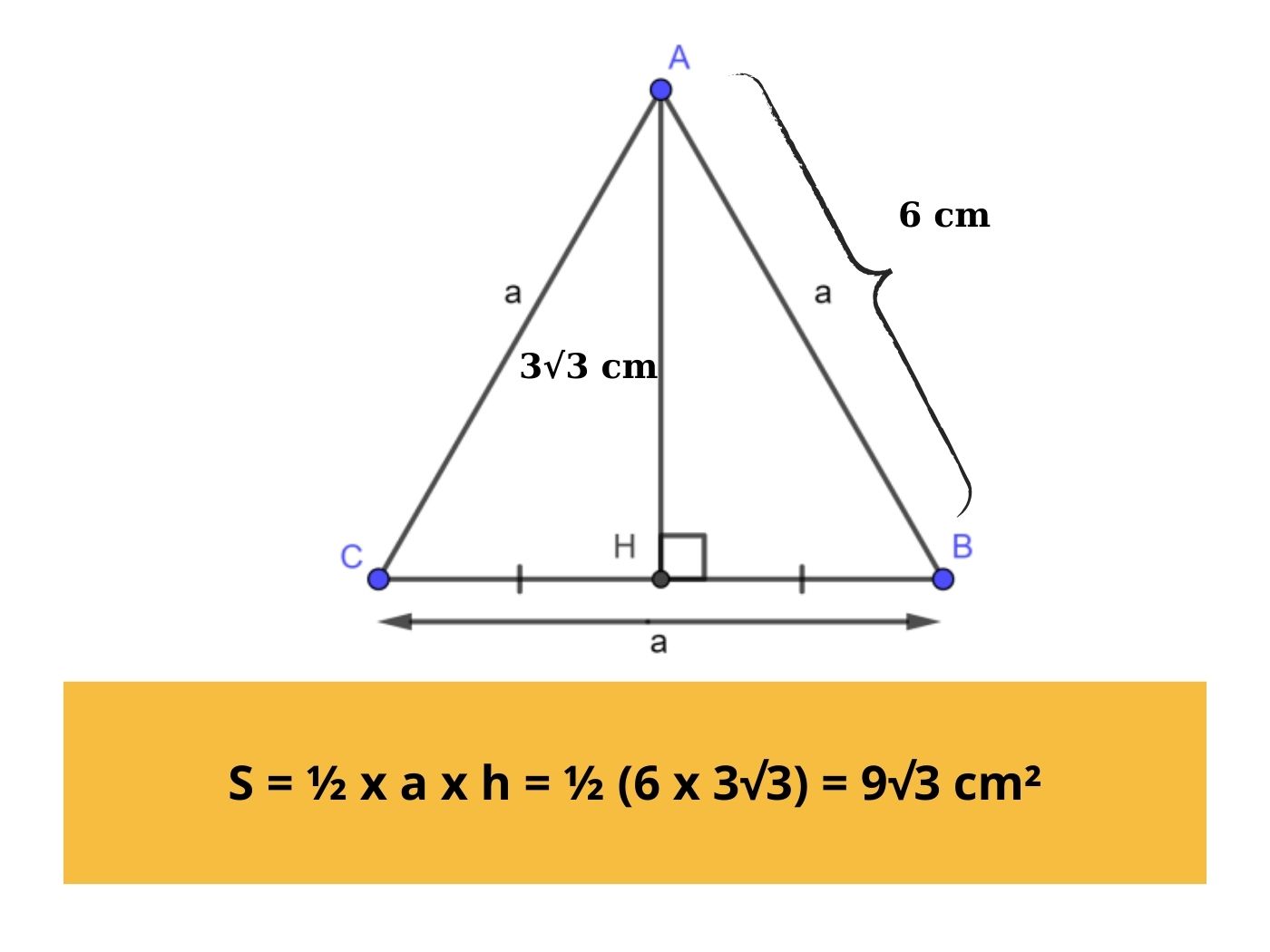Cách tính diện tích tam giác đều 

Xem thêm: Web Học Toán Online mới nhất, học tập hiệu quả cho mọi lứa tuổi

Cách tính diện tích tam giác vuông 

Tam giác vuông có một góc bằng 90 độ và 2 cạnh vuông góc gới nhau, khi đó tam giác vuông sẽ có công thức tính diện tích như sau: 

Công thức S = ½ x a x b 

Trong đó 

• S: Diện tích tam giác vuông 
• a, b: Độ dài hai cạnh góc vuông tương ứng. 

Ví dụ: Cho tam giác ABC vuông tại A có cạnh AB là 7cm và AC là 8cm, hãy tính diện tích tam giác ABC. 

Lời giải: Diện tích tam giác ABC được tính theo công thức  S = ½ x a x b = ½ (AB x AC) = ½ (7 x 8) = 28 cm2. 

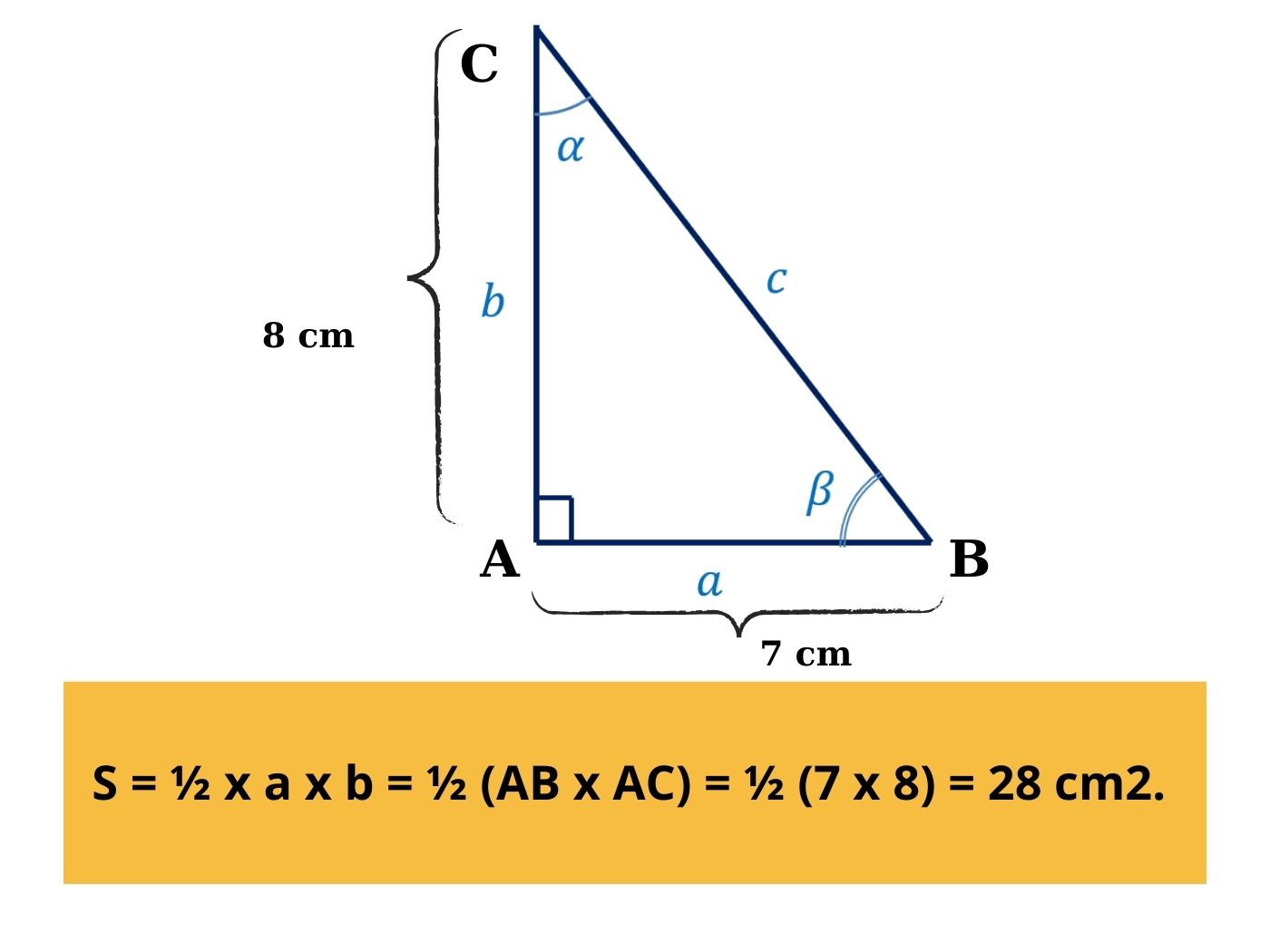Tính diện tích hình tam giác vuông

Một số công thức tính diện tích tam giác mở rộng 

Một số công thức mở rộng khi tính diện tích tam giác bạn có thể tham khảo và áp dụng khi làm bài tập dưới đây: 

Cách tính diện tích tam giác khi biết một góc 

Công thức tính diện tích tam giác khi biết một góc của tam giác bằng công thức 

S = (1/2) * a * b * sin(C) = S = (1/2) * a * c * sin(B) = S = (1/2) * c* b * sin(A). 

Trong đó: 

•  S: Diện tích tam giác
• a, b, c: Độ dài cạnh của tam giác
• A, B, C: Góc xen giữa hai cạnh

Ví dụ: Cho hình tam giác ABC có AB = 5cm, AC = 7cm và góc A = 60 độ  yêu cầu tính diện tích tam giác ABC. 

Lời giải: Áp dụng công thức S = (1/2) * AB * AC * sin(A)  => S = (1/2) * 5 * 7 * sin(60) = 15.19 cm².

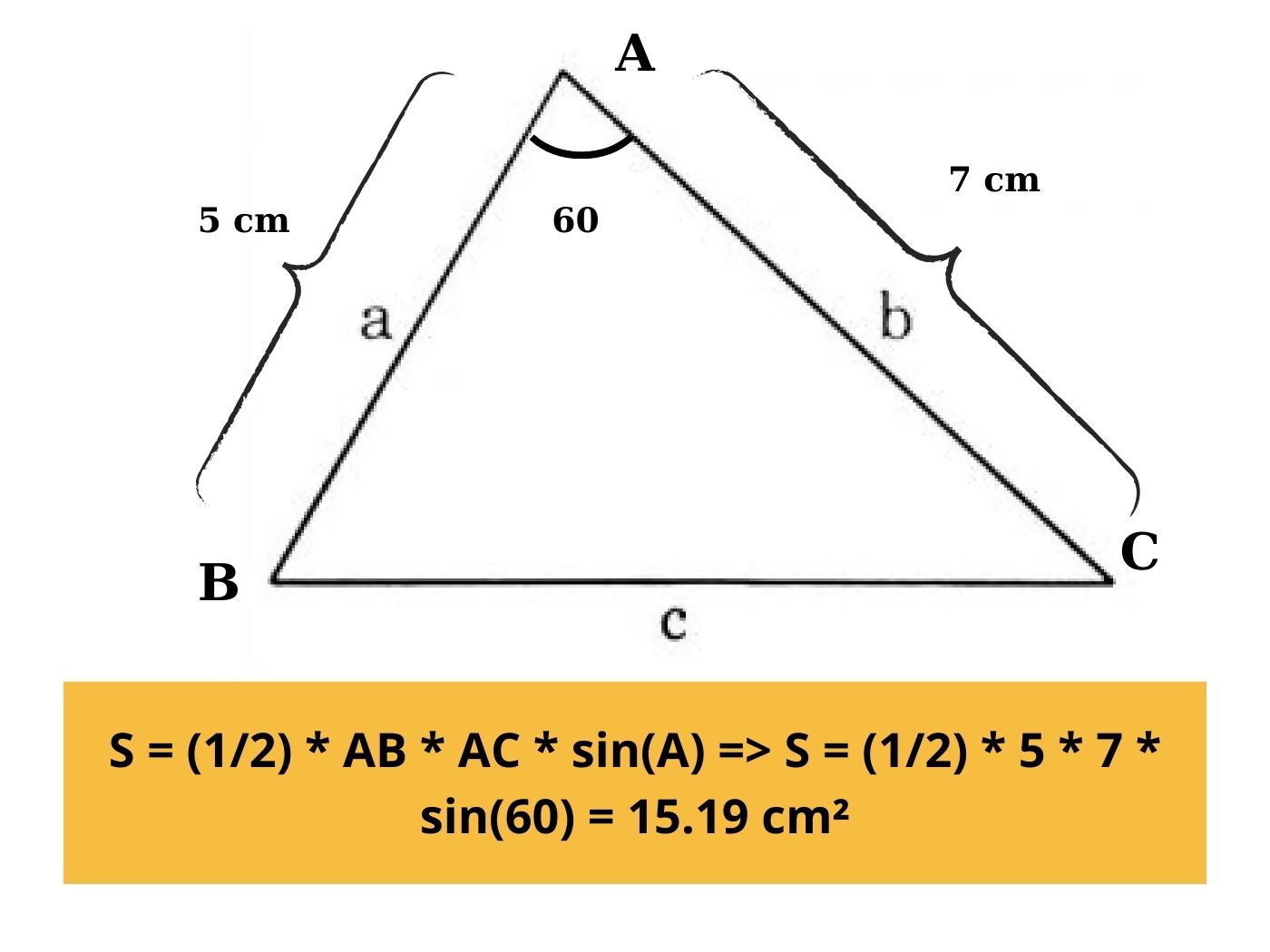Tính diện tích tam giác khi biết một góc

Cách tính diện tích tam giác khi biết 3 cạnh 

Công thức tính diện tích tam giác khi biết 3 cạnh của hình tam giác đó dưới đây: 

Công thức S = √[p(p-a)(p-b)(p-c)]

Trong đó: 

• S: Diện tích tam giác
• a, b, c: Độ dài ba cạnh của tam giác
• p: Nửa chu vi tam giác được tính theo công thức (p = (a+b+c)/2)

Ví dụ: Cho tam giác ABC có độ dài AB = 5cm, AC = 6cm và BC = 7cm, hãy tính diện tích tam giác ABC. 

Lời giải: Áp dụng công thức tính diện tích S = √[p(p-a)(p-b)(p-c)] ta có  p = (a+b+c)/2 = (5+7+6)/2 = 9 cm => S = √[9(9-5)(9-7)(9-6)] = √[942*3] ≈ 14.69 cm²

Cách tính diện tích tam giác bằng bán kính đường tròn ngoại tiếp 

Công thức tính diện tích tam giác bằng bán kính đường tròn ngoại tiếp tam giác R như sau:  S = (abc) / (4R). 

Trong đó: 

• S: Diện tích tam giác
• a, b, c: Độ dài ba cạnh của tam giác
• R: Bán kính đường tròn ngoại tiếp tam giác

Ví dụ: Cho hình tam giác ABC với AB = 5cm, AC = 6cm và BC = 7cm, biết bán kính đường tròn ngoại tiếp R = 3.5 hãy tính diện tích tam giác ABC. 

Lời giải: Áp dụng công thức  S = (abc) / (4R) ta có SABC = (AB x AC x BC)/4R = (5 * 7 * 6) / (4 * 3.5) = 15 cm2. 

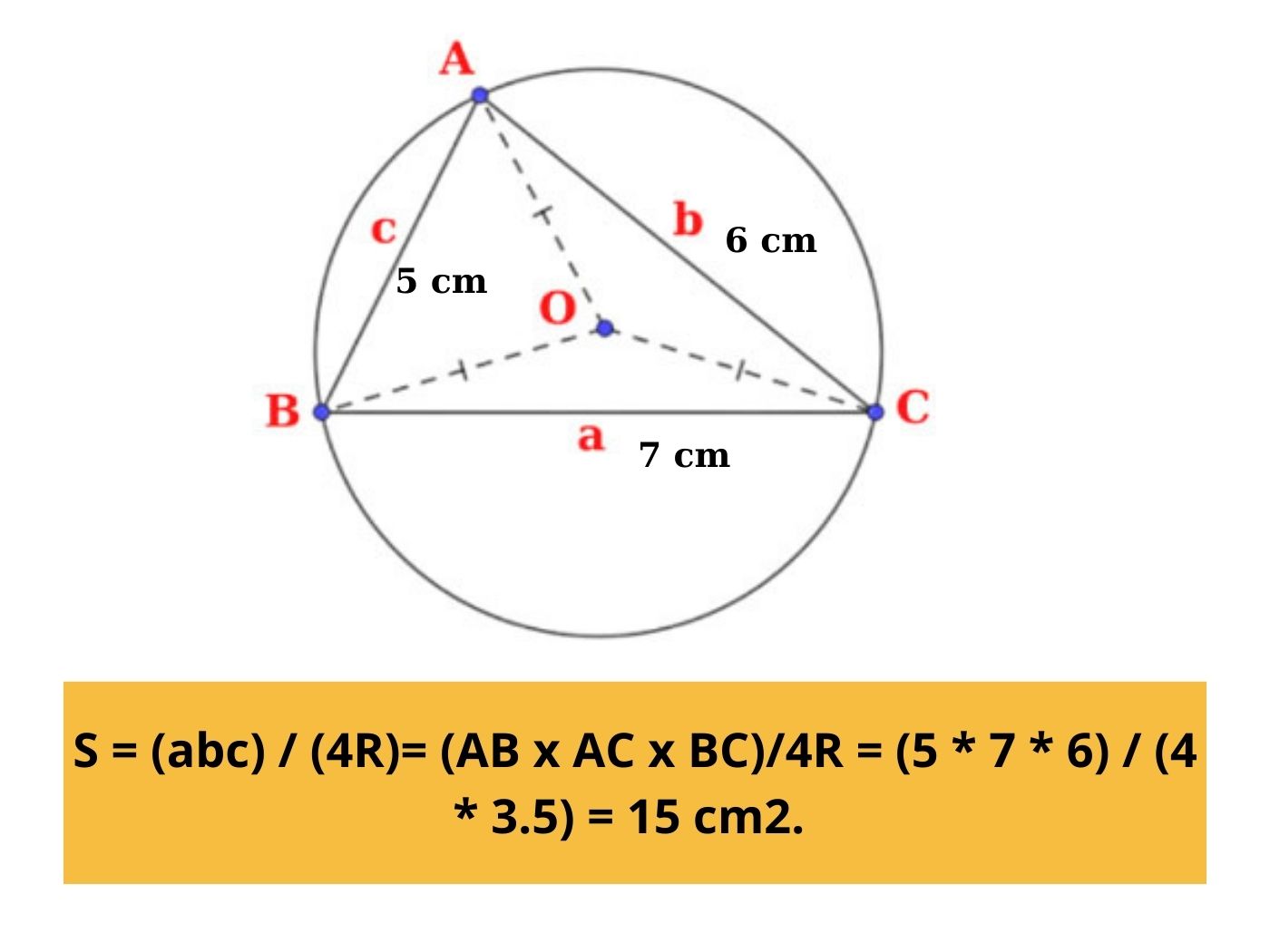Tính diện tích tam giác tâm bán kính đường tròn ngoại tiếp

Kết luận 

Như vậy công thức tính diện tích tam giác và những ví dụ thực tế đã được giải đáp chi tiết trong bài viết trên để bạn có thể theo dõi, áp dụng khi làm các dạng bài tập. Nếu muốn cập nhật thêm thông tin chi tiết về toán học, hãy theo dõi ngay g4me để được giải đáp nhanh chóng, chính xác nhất từ hôm nay nhé!